Hello! I have been doing some(some = 1 till now  ) experimentation on creating "localised noise generators".
) experimentation on creating "localised noise generators".
Why?
Let's say we want to make a single mountain using noise. We'll create a sparse facet and extend Borders to reserve a region for that mountain. But when we're sampling noise how can we guarantee that the mountain will remain confined to that region? A simple Perlin/Simplex noise function can cause discontinuities on the borders and there isn't any way to guarantee that a peak would occur inside the Border.
I wasn't able to find anything on the internet that aimed to solve such a problem, hence I thought of my own solution!
What I did to solve this?
I made a custom Perlin noise generator that guaranteed that the mountain would be restricted inside the region. It will be easier to explain with this diagram-
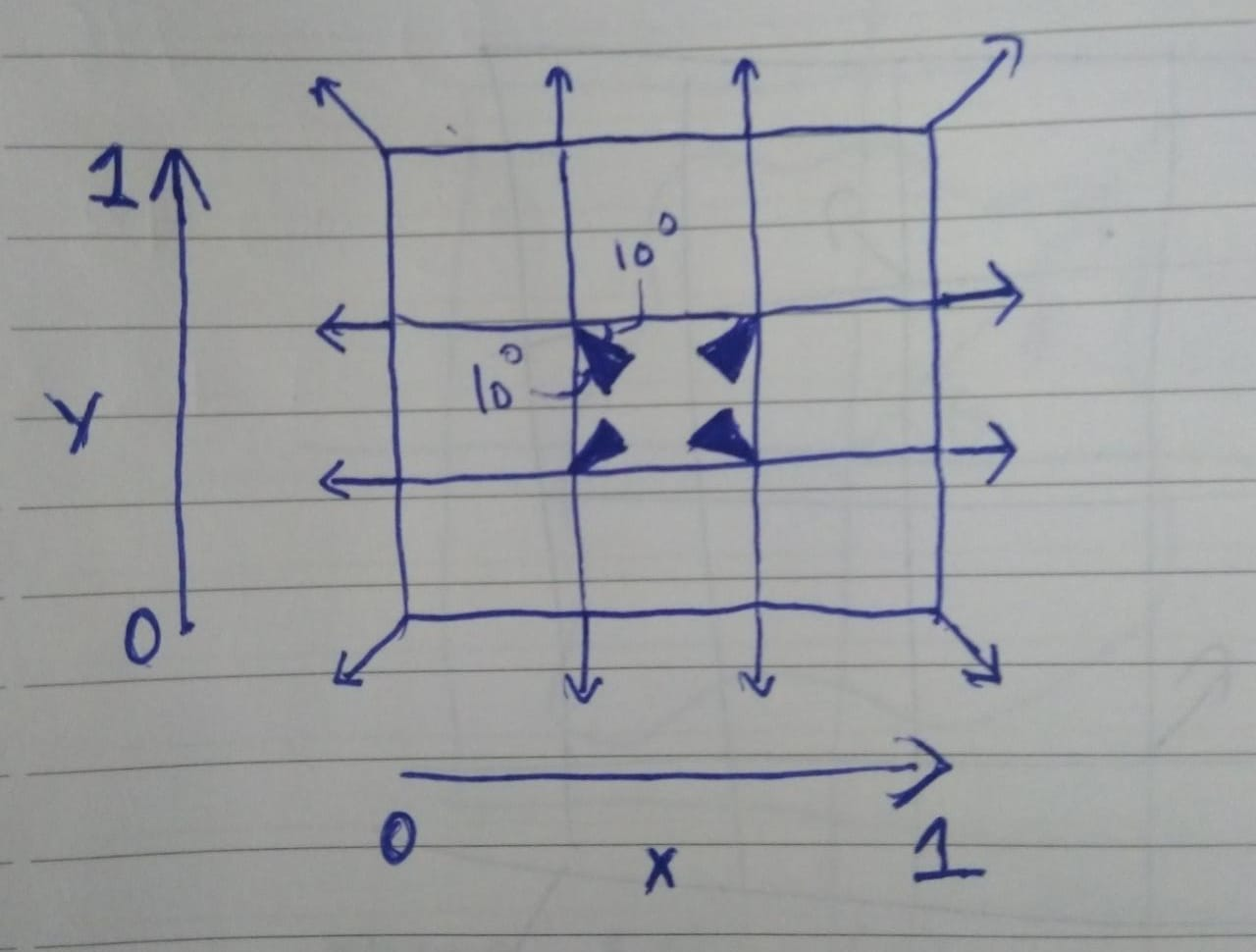
The noise generator accepts X and Y in [0,1] and divides the 1x1 region into a 3x3 grid system. Now the gradient vectors which are normally randomised for a Perlin generator are controlled here. The vectors lying on x=0,1 or y=0,1 have hardcoded "outward" directions which will ensure that the noise sampled reaches 0 before reaching the borders. Negative noise values are clamped to 0. The four vectors inside are chosen randomly with a restriction that they will always lie in the centre square and will be more than 10 degrees inclined from the sides of the central square, as shaded in the diagram.
Using this I wrote a world generator to create a single mountain, I got pretty good results

The mountains a bit protruded in the X and Z directions but that is because I didn't give the non-corner border vectors proper magnitude and directions
This PoC is available at- https://github.com/sin3point14/Terasology/tree/mountain-noise (notice the branch) and https://github.com/sin3point14/VolcanoTest
Now, from this, I propose 2 proper(hopefully?) noise generators for such things when we need to restrict a noise generator in a region-
Restricted Perlin/Simplex Noise Generator

The black grid will be a normal Perlin/Simplex generator and vectors on the yellow line will force the noise values to die to 0 before hitting the borders. The vectors on the black grid can again be manipulated in direction and magnitude as done in my mountain POC to create a guaranteed decreasing noise function which will surely die on the edges.
Its main features are-

This noise function is an amoeba-shaped(I don't know what else this could be called ) region, selector. Also, the noise value returns a value which gives a sense of the ratio of the distance of the sampled point from the centre to the cut-off contour.
) region, selector. Also, the noise value returns a value which gives a sense of the ratio of the distance of the sampled point from the centre to the cut-off contour.
Its main features are-
Both have different purposes and I'd like to hear everyone's views on this!
Also if anyone could give me some reading material that relates to this problem it would be great!
Why?
Let's say we want to make a single mountain using noise. We'll create a sparse facet and extend Borders to reserve a region for that mountain. But when we're sampling noise how can we guarantee that the mountain will remain confined to that region? A simple Perlin/Simplex noise function can cause discontinuities on the borders and there isn't any way to guarantee that a peak would occur inside the Border.
I wasn't able to find anything on the internet that aimed to solve such a problem, hence I thought of my own solution!
What I did to solve this?
I made a custom Perlin noise generator that guaranteed that the mountain would be restricted inside the region. It will be easier to explain with this diagram-
The noise generator accepts X and Y in [0,1] and divides the 1x1 region into a 3x3 grid system. Now the gradient vectors which are normally randomised for a Perlin generator are controlled here. The vectors lying on x=0,1 or y=0,1 have hardcoded "outward" directions which will ensure that the noise sampled reaches 0 before reaching the borders. Negative noise values are clamped to 0. The four vectors inside are chosen randomly with a restriction that they will always lie in the centre square and will be more than 10 degrees inclined from the sides of the central square, as shaded in the diagram.
Using this I wrote a world generator to create a single mountain, I got pretty good results

The mountains a bit protruded in the X and Z directions but that is because I didn't give the non-corner border vectors proper magnitude and directions
This PoC is available at- https://github.com/sin3point14/Terasology/tree/mountain-noise (notice the branch) and https://github.com/sin3point14/VolcanoTest
Now, from this, I propose 2 proper(hopefully?) noise generators for such things when we need to restrict a noise generator in a region-
Restricted Perlin/Simplex Noise Generator

The black grid will be a normal Perlin/Simplex generator and vectors on the yellow line will force the noise values to die to 0 before hitting the borders. The vectors on the black grid can again be manipulated in direction and magnitude as done in my mountain POC to create a guaranteed decreasing noise function which will surely die on the edges.
Its main features are-
- Gives a continuous region with multiple peaks.
- Frequency of noise can be controlled by controlling tesselation.
- The region isn't necessary to be rectangular we could have an arbitrary shaped region and vectors on its border(yellow box in the diagram) could be sampled to face along at the outward normal to ensure the noise dying out.

This noise function is an amoeba-shaped(I don't know what else this could be called
Its main features are-
- Requires a rectangular/radial region to be sampled upon.
- Will have one peak in the centre of the region.
- The "waviness" of the contour can be controlled by controlling the frequency of the Noise function used in the diagram.
Both have different purposes and I'd like to hear everyone's views on this!
Also if anyone could give me some reading material that relates to this problem it would be great!
